1.
(a)Following hint, try y = xp. Plugging into ODE:
(b) The general solution is then
y = C+xp+ + C-xp-,
and at x=1, y=0. Using this we obtain
C+ + C- =0. Therefore
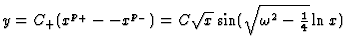 .
.
2. Write
y(x,t) = X(x)T(t) and plugging into
(b) At x=2, y=0, so
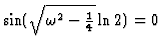 ,
which implies
,
which implies
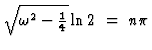 .
.
(c) Solving for ![]() ,
,
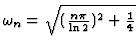 for
for
![]() .
.
(d) Summing over all solutions:
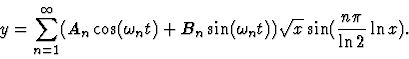
3.
![]() and
and
Try
![]() .
This implies
.
This implies
4. (a) From 1(b)
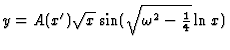 for x < x'.
for x < x'.
(b) Rescale x:
![]() ,
with the boundary condition
y(x/2) = 0. Therefore
C+ + C- =0, and so
,
with the boundary condition
y(x/2) = 0. Therefore
C+ + C- =0, and so
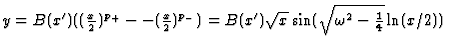 .
for x> x'.
.
for x> x'.
(c)
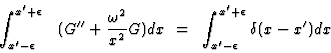
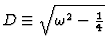 .
From continuity
.
From continuity
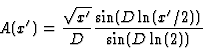
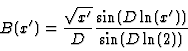
(e)
![]() .
.