


Next: About this document ...
Physics 120/240
Homework 1
Due 4/19/06
This homework has a lot of overlap with introductory statistical mechanics
that you've probably already seen, but it may very well bring a new
perspective to it.
One important thing to be learned from this is an understanding of the
applicability of the "Central Limit
Theorem". Where it works and where it doesn't.
Another thing is the relationship between what you already know and polymer
statistics.
The last part of this assignment is to implement the ideas in this problem numerically.
I encourage you to team up with others for some or all of this homework.
1. Consider 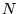 noninteracting Ising spins
noninteracting Ising spins
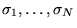 where each spin is
chosen with equal probabilities to have values
where each spin is
chosen with equal probabilities to have values 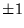 . The Hamiltonian (or
energy) of this system is
. The Hamiltonian (or
energy) of this system is
where 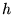 is some parameter that can be thought of as a (negative) magnetic field.
Using combinatorics (or the binomial distribution), calculate the number states
that the system can have at energy
is some parameter that can be thought of as a (negative) magnetic field.
Using combinatorics (or the binomial distribution), calculate the number states
that the system can have at energy 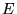 .
.
2. Define the entropy per spin
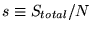 and the energy per spin as
and the energy per spin as
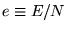 . Use the simplified Sterling's formula
. Use the simplified Sterling's formula
to find an expression form 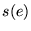 in the limit of large
in the limit of large 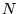 .
.
3. The result of the last problem is the entropy in the "microcanonical",
or constant energy, ensemble. Let's do the calculation in the "canonical",
or constant temperature, ensemble. Consider the same system but now held
at constant temperature.
- a
- The partition function
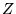 for this system can be easily calculated. Do this
by realizing that the spins are noninteracting so that the system breaks up
into
for this system can be easily calculated. Do this
by realizing that the spins are noninteracting so that the system breaks up
into 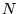 subsystems.
subsystems.
- b
- Now calculate the free energy
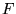 .
.
- c
- By the appropriate differentiation, calculate the energy
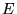 .
.
- d
- Recall that
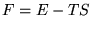 . From this and the answer to the last part, calculate
. From this and the answer to the last part, calculate 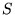 as a function of
as a function of 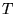 (or
(or 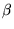 ). Then find
). Then find 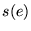 as before.
To do this, you'll have to invert a
as before.
To do this, you'll have to invert a 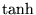 which can be expressed in terms of a
logarithm. Your result should be identical to the one found in the previous
problem.
which can be expressed in terms of a
logarithm. Your result should be identical to the one found in the previous
problem.
4.
- a
- Calculate
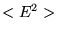 . The average is over all possible spin configurations
all of which are weighted equally. This can be thought of several different
ways. One is an average weighted by the probability distribution in problem 1.
This isn't the easiest way to calculate this. Instead write
. The average is over all possible spin configurations
all of which are weighted equally. This can be thought of several different
ways. One is an average weighted by the probability distribution in problem 1.
This isn't the easiest way to calculate this. Instead write 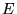 in terms of
the
in terms of
the 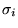 's which leads to a double sum. Using independence of the spins
the cross terms can be eliminated.
's which leads to a double sum. Using independence of the spins
the cross terms can be eliminated.
- b
- Calculate
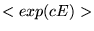 where
where 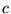 is an arbitrary constant. The easiest way to do
this is similar to part a; if
is an arbitrary constant. The easiest way to do
this is similar to part a; if 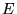 is expressed as a sum over spins, this can
then be written as a product (similar to the calculation of the partition
function). Using independence allows you to decouple all terms.
is expressed as a sum over spins, this can
then be written as a product (similar to the calculation of the partition
function). Using independence allows you to decouple all terms.
5. Find an expression for the probability distribution 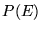 near
near 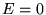 for
large
for
large 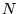 . Do this by expanding out the logarithms found in problem 2.
Hint: Make sure to go to 2nd order in the expansion of the logs!
Your result should be a Gaussian.
. Do this by expanding out the logarithms found in problem 2.
Hint: Make sure to go to 2nd order in the expansion of the logs!
Your result should be a Gaussian.
6. Using the Gaussian approximation of problem 5, recalculate the
averages of problem 4. The easiest way to do these is directly,
for example
Compare your results to the exact ones found in problem 4.
7. Do a rough sketch of
- a
- the exact
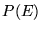 versus
versus 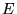 , and also
, and also 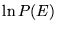 versus
versus 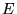 ,
,
- b
- the Gaussian approximation for both
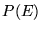 versus
versus 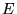 , and
, and 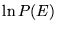 versus
versus 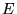 .
.
Display the essential features, such as the width of the distribution and
how the two cases differ.
8. Now explain qualitatively from the sketches in the last problem
why the approximate results found in problem 6 either work well, or don't.
9. How do the last eight problems relate to the problem of a random walk?
Find a mapping between a random walk and the spin system discussed above.
How is the force related to the "spin" 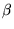 found before?
found before?
10. Calculate the probability distribution of a random walk this numerically as follows.
- a
- Write a program that generates a random sequences of
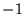 's and
's and 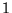 's and sums
's and sums
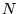 of them up at a time. You don't have to use the best random number generator
in the assignment, for example, you can use the unix "rand" function. Be careful
however not to do something like rand()%2. That is a big no no. Instead
you want something that divides by the right big number to first create a random
number that goes between
of them up at a time. You don't have to use the best random number generator
in the assignment, for example, you can use the unix "rand" function. Be careful
however not to do something like rand()%2. That is a big no no. Instead
you want something that divides by the right big number to first create a random
number that goes between
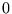 and
and 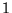 . Use that to decide if the answer should be
. Use that to decide if the answer should be 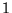 or
or 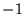 . This (ran())
and many useful macros are defined in Josh's
defs.h
. This (ran())
and many useful macros are defined in Josh's
defs.h
- b
- Take the resulting sum and assign it to a "bucket" which takes the
form of an array. You can allocate all the memory it uses in advance,
or do so dynamically using a more general scheme such as Josh's
hist.c
and
hist.h
- c
- After enough averages, you should be able to plot your histogram
by writing it to a file and using gnuplot or some other graphing tool.



Next: About this document ...
Joshua Deutsch
2004-01-07
![]() noninteracting Ising spins
noninteracting Ising spins
![]() where each spin is
chosen with equal probabilities to have values
where each spin is
chosen with equal probabilities to have values ![]() . The Hamiltonian (or
energy) of this system is
. The Hamiltonian (or
energy) of this system is

![]() and the energy per spin as
and the energy per spin as
![]() . Use the simplified Sterling's formula
. Use the simplified Sterling's formula
![]() near
near ![]() for
large
for
large ![]() . Do this by expanding out the logarithms found in problem 2.
Hint: Make sure to go to 2nd order in the expansion of the logs!
Your result should be a Gaussian.
. Do this by expanding out the logarithms found in problem 2.
Hint: Make sure to go to 2nd order in the expansion of the logs!
Your result should be a Gaussian.
![]() found before?
found before?