where
Take ![]() to be a scalar. The extension to the vector case is straightforward.
This problem illustrates how to calculate
to be a scalar. The extension to the vector case is straightforward.
This problem illustrates how to calculate
![]() , and
, and
![]() .
.
- Define the Fourier transform with respect to both
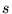 and
and 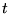 of
of 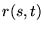 , Call it
, Call it
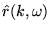 . Write down the inverse, that is, how to express
. Write down the inverse, that is, how to express 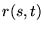 in terms
of integrals of
in terms
of integrals of 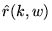 . Do the same for
. Do the same for 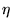 . Call the result
. Call the result 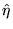 .
.
- Fourier transform equation 1 to obtain an algebraic equation.
- Fourier transform eqn. 2 with respect
to two sets of variables
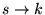 and
and
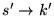 and similarly for
and similarly for
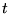 and
and 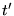 . Calculate
. Calculate
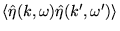 .
.
- Solve for
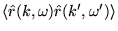 .
.
- Consider
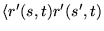 , where
, where
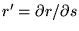 .
Relate this to
.
Relate this to
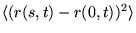 , through an integral formula.
, through an integral formula.
- Relate the Fourier transform of
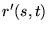 to
to 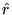 through the simple relation between
the Fourier transform of a function and its derivative.
through the simple relation between
the Fourier transform of a function and its derivative.
- Because the Rouse equation is translationally invariant in time, we can set
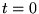 and
calculate instead
and
calculate instead
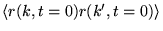 . Calculate this by expressing it in terms of integrals over
. Calculate this by expressing it in terms of integrals over
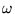 and
and 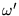 .
.
- Transform back to obtain
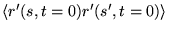 .
.
- From this obtain
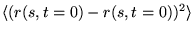 using part 5.
using part 5.
- Compare this with the prediction for
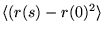 according to the equilibrium
statistical mechanics of a random walk.
according to the equilibrium
statistical mechanics of a random walk.
- Follow a similar procedure to obtain
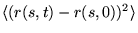 . Note that there
is translational invariance in arclength also so that you can set
. Note that there
is translational invariance in arclength also so that you can set 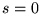 .
.