


Next: About this document ...
Physics 219
Homework 2
Read Reif Chapter 3 and do Reif problems 3.2, 3.4, 3.5.
Read Sethna Chapter 3, then do:
1. Consider the simulation shown
here
of two circular disks of mass 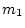 and
and 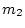 and radii
and radii 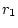 and
and 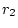 that
move in a two dimensional square container of length
that
move in a two dimensional square container of length 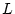 . Initially the energy of the first one is
. Initially the energy of the first one is
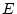 and the second is
and the second is 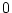 . There is no dissipation and no rotational motion of
the disks. Calculate
. There is no dissipation and no rotational motion of
the disks. Calculate
 |
(1) |
Here 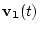 is the velocity vector of the first particle as a function
of time.
is the velocity vector of the first particle as a function
of time.
2. Consider an ideal gas in isolation with total energy 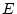 of
of 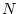 identical
particles with mass
identical
particles with mass 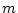 .
The walls of the container are very heavy so that internal momentum
of the gas particles is not conserved.
.
The walls of the container are very heavy so that internal momentum
of the gas particles is not conserved.
- (a)
What is the time average
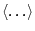 of
of
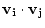 ? That is, calculate
? That is, calculate
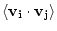 .
Do this for
.
Do this for 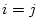 and
and 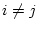 . Symmetry arguments give
the answers in a couple of lines.
. Symmetry arguments give
the answers in a couple of lines.
- (b)
Now consider a situation where momentum is conserved.
The walls could be very light (massless) compared to the mass of gas inside
as with a balloon and the balloon is in a vacuum. Adding
in conservation of momentum, to restrict the region of allowable
motion in phase space, what happens to your answers for part (a)?
3. A classical gas of dumbbells. A dumbbell consists of
2 equal masses 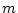 separated by a distance
separated by a distance 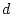 that rotate freely
in three dimensions. Consider a dilute gas of
that rotate freely
in three dimensions. Consider a dilute gas of 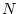 of these in a volume
of these in a volume 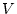 and assume that the interaction between them is negligible.
and assume that the interaction between them is negligible.
- (a)
By starting with the kinetic energy of a dumbbell, obtain its Lagrangian,
in terms of angular variables. Then obtain the canonical momenta and from
that the Hamiltonian. When you do this it is easier to ignore the translation part
and just consider the rotational part. You then add in the translational
center of mass kinetic energy later.
- (b)
From the Hamiltonian, calculate the heat capacity using the basic assumption
relating entropy to the number of accessible states, Reif eqn (3.3.12).



Next: About this document ...
Joshua Deutsch
2005-04-06
![]() and
and ![]() and radii
and radii ![]() and
and ![]() that
move in a two dimensional square container of length
that
move in a two dimensional square container of length ![]() . Initially the energy of the first one is
. Initially the energy of the first one is
![]() and the second is
and the second is ![]() . There is no dissipation and no rotational motion of
the disks. Calculate
. There is no dissipation and no rotational motion of
the disks. Calculate
![]() of
of ![]() identical
particles with mass
identical
particles with mass ![]() .
The walls of the container are very heavy so that internal momentum
of the gas particles is not conserved.
.
The walls of the container are very heavy so that internal momentum
of the gas particles is not conserved.
![]() separated by a distance
separated by a distance ![]() that rotate freely
in three dimensions. Consider a dilute gas of
that rotate freely
in three dimensions. Consider a dilute gas of ![]() of these in a volume
of these in a volume ![]() and assume that the interaction between them is negligible.
and assume that the interaction between them is negligible.