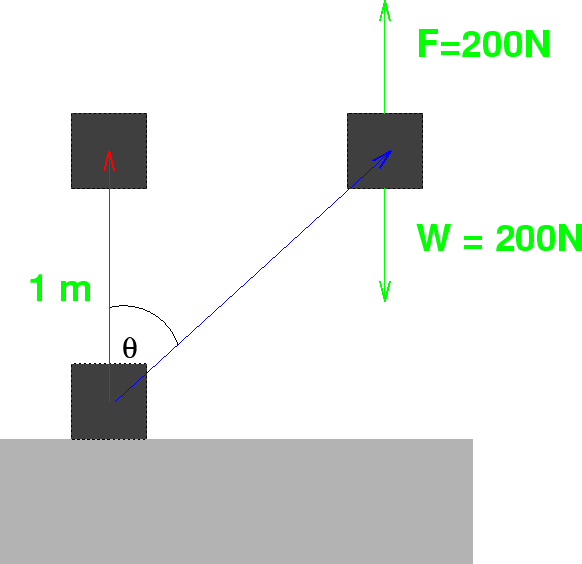
Imagine you have to lift a crate off the ground by 1 meter. The crate weighs 200 N. The idea of work is that you have to apply a force of 200N to the box in order to lift it. The work you do is just this force, 200 N times the distance you move it, 1 meter. So the work you do is 200 Nm. We'll define a new unit called a ``Joule'' (J) which is a Newton times a meter. So you do 200 J lifting this crate vertically up.
This is illustrated in the figure below by the red arrow:
Now suppose you don't move it vertically up but at some
angle ![]() with respect to the vertical,
as illustrated by the blue arrow.
So you still end up 1 meter higher than where you started
but some distance away horizontally. we are defining
work, we'll want the work to be the same. So the work you do is
the force times the distance gone in the direction of the force.
The force
with respect to the vertical,
as illustrated by the blue arrow.
So you still end up 1 meter higher than where you started
but some distance away horizontally. we are defining
work, we'll want the work to be the same. So the work you do is
the force times the distance gone in the direction of the force.
The force ![]() is vertically upward and the vector representation
of the distance traveled is the blue arrow. So how do we come
up with a nice concise definition of work involving vectors?
It's easy with the dot product. We just take the dot product
of the blue displacement vector
is vertically upward and the vector representation
of the distance traveled is the blue arrow. So how do we come
up with a nice concise definition of work involving vectors?
It's easy with the dot product. We just take the dot product
of the blue displacement vector
![]() with the force
with the force
![]() . So the work is
. So the work is
| (1.1) |
This is the definition of work when you have a force that doesn't change as you move, and also the path you take is straight. We'll now consider in one dimension how the work is related to velocity and introduce the concept of kinetic energy.