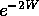 , where
, where
Debye Waller factor
The intensity of Bragg scattering is reduced, due to motion of atoms about their
equilibrium positions, by the Debye-Waller factor, generally written as
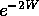 , where
, where
The average is evaluated
in the harmonic approximation,
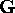 is a reciprocal lattice vector, and
is a reciprocal lattice vector, and
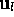 is the displacement of the l-th atom.
The average in Eq. (1) is trivially found from
the result
is the displacement of the l-th atom.
The average in Eq. (1) is trivially found from
the result
where  denotes a quantum statistical mechanical
average at a
temperature
denotes a quantum statistical mechanical
average at a
temperature 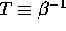 for a simple harmonic oscillator (or set of oscillators), and
A is a linear combination of the displacements and momenta of the oscillators
(or, equivalently, a linear combination of creation and destruction operators),
i.e.
for a simple harmonic oscillator (or set of oscillators), and
A is a linear combination of the displacements and momenta of the oscillators
(or, equivalently, a linear combination of creation and destruction operators),
i.e.

We now proceed to prove Eq. (2).
The most commonly given proofs of Eq. (2) are quite cumbersome, but Mermin, J. Math. Phys. 7, 1038 (1966) has a compact derivation which we follow here. To begin with, consider just a single oscillator, and let us evaluate
where a and b are constants and
c and 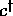 are creation and annihilation operators for an
oscillator with Hamiltonian
are creation and annihilation operators for an
oscillator with Hamiltonian
We start with the well known formula
assuming that the commutator 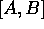 is a c-number. A derivation of this is
given in the Appendix. Applying Eq. (6) to Eq. (4) gives
is a c-number. A derivation of this is
given in the Appendix. Applying Eq. (6) to Eq. (4) gives
We can also apply Eq. (6) to Eq. (4) but with the opposite identification of A and B to give
Eqs. (7) and (8) are consistent only if
where the last line follows from the cyclic invariance of the trace. Expanding
out the 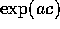 in the last line one can sandwich factors of
in the last line one can sandwich factors of 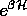 and
and 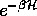 around each factor of c and so
around each factor of c and so

where
where the last line is derived in the Appendix. Hence we have

Iterating this procedure another n times we have
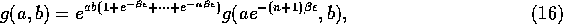
and so taking the limit 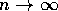 we have
we have

Now trivially,

since all terms in the expansion of the exponential give zero except the first. Hence
where

is the Planck distribution, and so from Eqs. (7), (9) and (19), we obtain
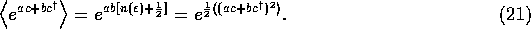
The derivation goes over straightforwardly to the case where there are many operators and so we obtain Eq. (2).
As a result of Eq. (2), the Debye Waller factor is given by
where

This expression is evaluated by transforming to k-space, so

where s denotes a branch. For simplicity we assume a Bravais lattice, ( i.e. just one atom per unit cell) and so writing

where 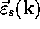 is the polarization vector and
M is the mass of the ion, we have
is the polarization vector and
M is the mass of the ion, we have
Our final result, then, is that
the intensity of a Bragg peak is reduced, due to the motion of the atoms,
by the Debye Waller factor, 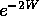 ,
where W is given by Eq. (26).
,
where W is given by Eq. (26).
Note:
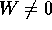 even at T=0 because of the zero point motion of the atoms.
even at T=0 because of the zero point motion of the atoms.
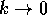 .)
Since the amplitude of the
Bragg peak is proportional to
.)
Since the amplitude of the
Bragg peak is proportional to  then there are no (delta-function)
Bragg peaks in two dimensions. In other words there is no long range
crystalline order at finite-T in two dimensions. Because of thermal
fluctuations, positional order is eventually lost at long distances, though
locally there will be a good crystalline arrangement. This was known in the
1930's through the work of Landau (see Landau and Lifshitz, Statistical
Mechanics), and Peierls, (Quantum Theory of Solids) and was made rigorous in the
1960's through the work of Mermin, Wagner, and Hohenberg, see especially
N.D. Mermin. J. Math. Phys. 8 1061 (1967). Since the divergence is weak,
and since it turns out that there is long range orientational order, see
Halperin and Nelson, Phys. Rev. 19, 2467 (1979), the delta function Bragg
peaks are replaced by cusp-like divergences of the form
then there are no (delta-function)
Bragg peaks in two dimensions. In other words there is no long range
crystalline order at finite-T in two dimensions. Because of thermal
fluctuations, positional order is eventually lost at long distances, though
locally there will be a good crystalline arrangement. This was known in the
1930's through the work of Landau (see Landau and Lifshitz, Statistical
Mechanics), and Peierls, (Quantum Theory of Solids) and was made rigorous in the
1960's through the work of Mermin, Wagner, and Hohenberg, see especially
N.D. Mermin. J. Math. Phys. 8 1061 (1967). Since the divergence is weak,
and since it turns out that there is long range orientational order, see
Halperin and Nelson, Phys. Rev. 19, 2467 (1979), the delta function Bragg
peaks are replaced by cusp-like divergences of the form
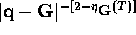 , where
, where  is an
exponent which varies with T and G.
is an
exponent which varies with T and G.
First of all we will derive Eq. (14), i.e. \
where 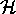 is the free particle Hamiltonian in Eq. (5).
Defining
is the free particle Hamiltonian in Eq. (5).
Defining
and differentiating with respect to  gives
gives
Solving this equation with the boundary condition 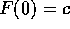 gives
Eq. (14).
gives
Eq. (14).
Finally, we derive Eq. (6). Let us write

where  is a c-number. Then
is a c-number. Then

and, differentiating with respect to  gives
gives
We evaluate the commutator
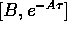 using the result
using the result

valid if 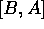 is a c-number,
which is obtained by successively moving the factor of B through the n
factors of A one place at a time. Hence
is a c-number,
which is obtained by successively moving the factor of B through the n
factors of A one place at a time. Hence

where F is any function, and the prime denotes a derivative. For the case of interest here, this gives

Substituting into Eq. (34) then gives
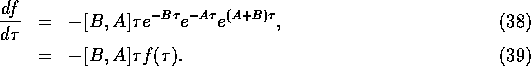
Integrating, and using the boundary condition that  , which is obvious,
gives the desired result, Eq. (6).
, which is obvious,
gives the desired result, Eq. (6).