How does all this go over into three dimensions?
One now needs to add ![]() , so
the semi-classical orbits, which were circles in two dimensions, are
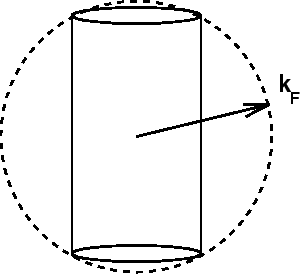
now cylinders. One such cylinder is shown in Fig. 6. As
, so
the semi-classical orbits, which were circles in two dimensions, are
now cylinders. One such cylinder is shown in Fig. 6. As ![]() increases
the radius increases.
However, one does not expect a dramatic change in
the magnetization until the radius increases to
increases
the radius increases.
However, one does not expect a dramatic change in
the magnetization until the radius increases to ![]() ,
(shown dashed in Fig. 6),
beyond which the cylinder
does not intersect the Fermi sphere at all. When the cylinders "pop out" of
the Fermi sphere one expects oscillatory behavior in the magnetization just as
in two dimensions. This can be confirmed by a mathematical analysis, see e.g.
Peierls, pp. 144-149. Clearly then, the periodicity of the magnetization with
,
(shown dashed in Fig. 6),
beyond which the cylinder
does not intersect the Fermi sphere at all. When the cylinders "pop out" of
the Fermi sphere one expects oscillatory behavior in the magnetization just as
in two dimensions. This can be confirmed by a mathematical analysis, see e.g.
Peierls, pp. 144-149. Clearly then, the periodicity of the magnetization with
![]() involves the maximum area formed by the intersection of the Fermi sphere with
a plane perpendicular to
involves the maximum area formed by the intersection of the Fermi sphere with
a plane perpendicular to ![]() . If one has a general Fermi surface from some
complicated band structure, then it is also possible that, on varying
. If one has a general Fermi surface from some
complicated band structure, then it is also possible that, on varying ![]() , the
intersection of the Fermi surface with the plane of constant
, the
intersection of the Fermi surface with the plane of constant ![]() might have a
minimum. These orbits will also contribute to the oscillatory behavior
because the part of the cylinder inside the Fermi sphere will decrease rapidly
when the radius of the cylinder passes this extremal radius.
might have a
minimum. These orbits will also contribute to the oscillatory behavior
because the part of the cylinder inside the Fermi sphere will decrease rapidly
when the radius of the cylinder passes this extremal radius.
 |
Thus we conclude that the magnetization will show
oscillations with periods given by
A determination of oscillations in ![]() as a function of
as a function of ![]() (the de Haas-van
Alphen effect) for different orientations orientations of the field has been
the most successful method for mapping out the shape of the Fermi surface of
metals. It is discussed in AM, Ch. 14
(the de Haas-van
Alphen effect) for different orientations orientations of the field has been
the most successful method for mapping out the shape of the Fermi surface of
metals. It is discussed in AM, Ch. 14