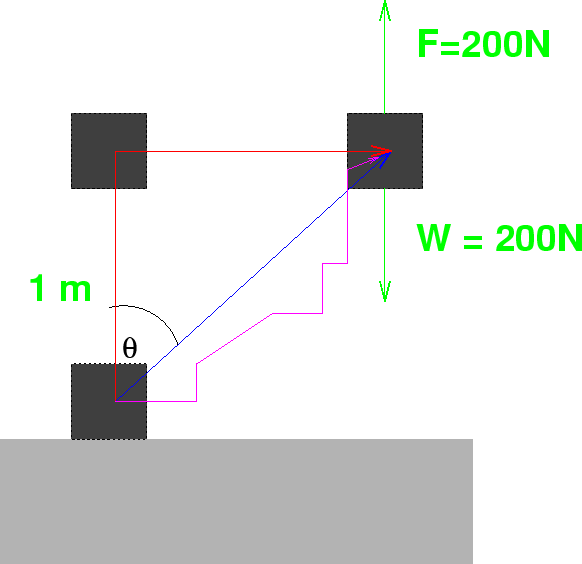
Recall the crate example we began this chapter with (1.2). The work done lifting the object straight up was the same as lifting to the same height at a different angle. Now what happens if we want the final position of the crate to be the same in both case, as illustrated below?
Well basically nothing changes, because the work along the horizontal part of the red line is zero, so again, the work for these two paths are the same. In fact you could choose the magenta path and you'd get exactly the same answer. You should be able to show this by reasoning similar to how we saw that the red and blue path gave the same work.
This force, the gravitational force, is an example of a conservative force. It doesn't matter what path you take, to go between two points, the work is always the same if you have a conservative force.
Another example of a conservative force is the force of a spring, from eq. 1.7 we see that it depends on only the end points which means that it must be conservative.
You can easily convince yourself the work done by a conservative force going on a closed path, that is one where the beginning and end points are the same, is zero. Give it a try!
What about the force of friction? Is that conservative? Well if you go around the room in a big circle pushing a crate on a rough surface and end up where you started, do you do any work? Of course you do. The work is the circumference times the frictional force. Therefore this can't be a conservative force.