Because this problem explicitly involves forces, conservation of energy alone can't be sufficient to solve this problem. But we've seen from the pendulum example above it is extremely powerful and so we'll use it in addition to Newton's laws.
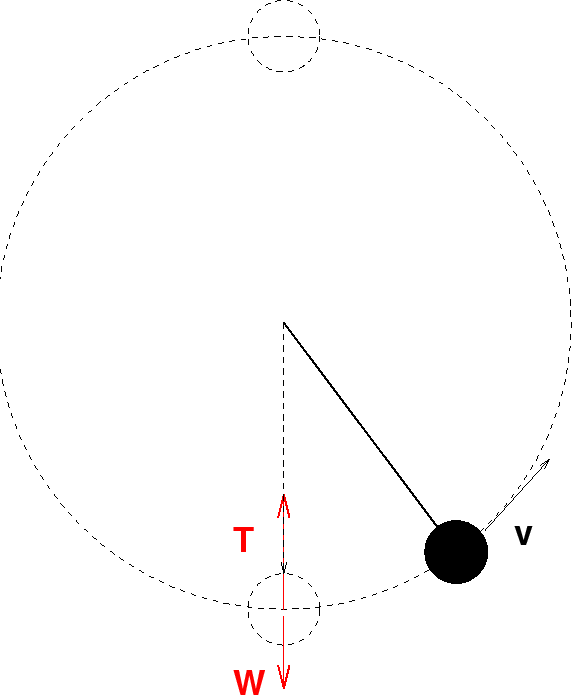
So how about Newton's laws applied to the ball at
the bottom? Well
![]() . What's
the acceleration? It's not zero because the ball
is traveling around in a circle. We know that
it points up and has a magnitude of
. What's
the acceleration? It's not zero because the ball
is traveling around in a circle. We know that
it points up and has a magnitude of ![]() .
What's the net force? The tension points up, but
the weight
.
What's the net force? The tension points up, but
the weight ![]() goes down so we have
goes down so we have
| (1.21) |
The tension at the top is similar but we have to realize though
that the acceleration and the tension are now both pointing in
the opposite directions what what they were on the bottom, so
| (1.22) |
We were asked for the difference between these tensions so
adding these equations, we have
So this is all we'll use of Newton's laws. Now we need to
figure out
![]() , which looks awfully closely
related to kinetic energy, so now we'll use conservation
of energy to figure it out.
, which looks awfully closely
related to kinetic energy, so now we'll use conservation
of energy to figure it out.
Let's define our coordinate system so that ![]() at the bottom of the circle.
Then the energy at the bottom is
at the bottom of the circle.
Then the energy at the bottom is
![]() ,
and the energy at the top is
,
and the energy at the top is
![]() .
Equating these two energies, we see that
.
Equating these two energies, we see that
| (1.24) |
Using this is eq. 1.23 we have
| (1.25) |
which is what we wanted to show.
Again this problem would be possible, but very hard to solve using Newton's laws alone.