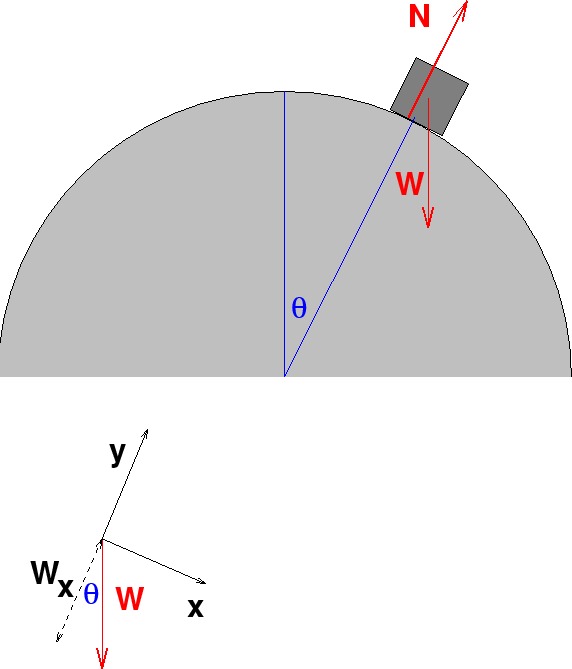
Another problem where conservation of energy is useful.
We draw a picture of the situation below
The red arrows represent a free body diagram of the block.
There are two forces, the weight and the normal force. What's the condition for when the block looses contact with the sphere? It's when the normal force is zero.
So lets apply Newton's laws to this situation. When the
normal force is zero, there's only one force, that is
gravity acting on the block. Using the coordinate
system shown, we'll calculate component of the acceleration in the y direction.
It is negative along the
y direction and has a magnitude of ![]() , i.e. the centripetal acceleration.
The component of gravity in the y direction is, from the diagram,
, i.e. the centripetal acceleration.
The component of gravity in the y direction is, from the diagram,
![]() . So from Newton's second law we have
. So from Newton's second law we have
| (1.26) |
or
Now let's use conservation of energy, choosing that the
potential energy is zero at the center of the sphere.
Then we have initially ![]() and finally
and finally
![]() . Eliminating
. Eliminating
![]() , we have
, we have
| (1.28) |
Now using eq. 1.27 this gives
| (1.29) |
Doing a little algebra this gives
![]() .
This is a height of
.
This is a height of
| (1.30) |