


Next: Three dimensions and the
Up: magnetic_field
Previous: Two dimensions, free electrons
Two dimensions, Bloch electrons
So far we have derived Eq. (32) only for free electrons in two
dimensions. The same result is also true for Bloch electrons (i.e. electrons in
a periodic potential) as we shall now show. Already that the
fact that it does not depend on the electron mass, which could be altered to
an effective mass by band structure effects, gives one a suspicion that this
might be so. In this section we still consider two dimensions.
The first stage in the proof is to derive Ashcroft and Mermin, Eq. (12.42),
relating the period of an orbit of a Bloch electron in a magnetic field to the
change in the area of the orbit with energy. We start with the semi-classical
equations of motion:
from which it follows that
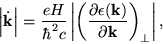 |
(40) |
where
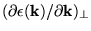 is the component of
is the component of
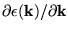 perpendicular to the
field, i.e.
its projection in the plane of the orbit. (Note this projection is not
necessary in two dimensions considered here, but we include it so that our
derivation of Eq. (44) below will also apply in three dimensions.)
Hence the period of an orbit is given by
perpendicular to the
field, i.e.
its projection in the plane of the orbit. (Note this projection is not
necessary in two dimensions considered here, but we include it so that our
derivation of Eq. (44) below will also apply in three dimensions.)
Hence the period of an orbit is given by
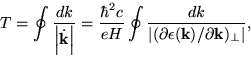 |
(41) |
where 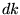 is the magnitude of a small element of the orbit, and
we integrate around the closed orbit.
If we consider
two
orbits whose difference in energy
is the magnitude of a small element of the orbit, and
we integrate around the closed orbit.
If we consider
two
orbits whose difference in energy
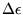 is small then the region
between them in the
is small then the region
between them in the 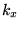 -
-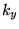 plane
is a ribbon of width
plane
is a ribbon of width
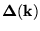 , see AM Fig. 12.9,
where
, see AM Fig. 12.9,
where
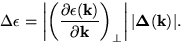 |
(42) |
Hence the period 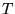 can be written as
can be written as
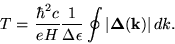 |
(43) |
The integral in the last equation is just the area between the two neighboring
orbits, 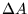 , and so
, and so
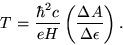 |
(44) |
Note that with a free electron band structure,
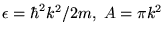 , this gives
, this gives
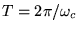 , where
, where 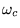 is the cyclotron frequency, as expected.
is the cyclotron frequency, as expected.
The second stage of the proof is to use another relationship involving the
period of the orbits, the Bohr-Sommerfeld correspondence principle, which
states that if 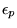 and
and
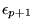 are two adjacent
energy levels with quantum numbers
are two adjacent
energy levels with quantum numbers 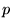 and
and 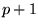 where
where 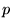 is assumed large,
then
is assumed large,
then
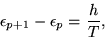 |
(45) |
where 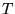 is the period of the motion of a semiclassical wavepacket on an orbit
with energy centered on
is the period of the motion of a semiclassical wavepacket on an orbit
with energy centered on 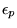 . This can be derived by noting that
the wavepacket is built up out of adjacent energy levels, and its
motion comes from interference
between different levels. This requires that the levels around
. This can be derived by noting that
the wavepacket is built up out of adjacent energy levels, and its
motion comes from interference
between different levels. This requires that the levels around 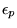 be uniformly spaced with spacing
be uniformly spaced with spacing
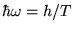 , where
, where 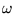 is the
angular frequency of the orbit.
(Note that the ``correspondence principle'' really only
comes in with the
further remark that
is the
angular frequency of the orbit.
(Note that the ``correspondence principle'' really only
comes in with the
further remark that 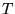 is also the period of a purely classical
particle of the same energy.)
is also the period of a purely classical
particle of the same energy.)
Applying this relation to Eq. (44) in which
we take
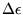 to be the difference in energy between adjacent
Landau levels,
to be the difference in energy between adjacent
Landau levels,
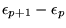 , then the area between the
semiclassical orbits of two adjacent
Landau levels
is given by
, then the area between the
semiclassical orbits of two adjacent
Landau levels
is given by
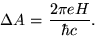 |
(46) |
This elegant result, first obtained by Onsager,
can be reexpressed by stating that at large 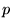 the area
the area 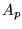 inside the
Landau level
inside the
Landau level 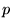 is given by
is given by
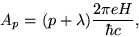 |
(47) |
where 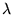 is some number independent of
is some number independent of 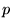 .
This is the same as Eq. (35) for free electrons, except that
.
This is the same as Eq. (35) for free electrons, except that 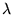 need not equal 1/2. The periodicity in
need not equal 1/2. The periodicity in 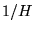 in Eq. (37),
obtained from Eq. (35), follows equally from Eq. (47).
in Eq. (37),
obtained from Eq. (35), follows equally from Eq. (47).



Next: Three dimensions and the
Up: magnetic_field
Previous: Two dimensions, free electrons
Peter Young
2002-10-31
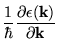
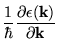
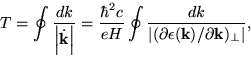
![]() and
and
![]() are two adjacent
energy levels with quantum numbers
are two adjacent
energy levels with quantum numbers ![]() and
and ![]() where
where ![]() is assumed large,
then
is assumed large,
then
![]() to be the difference in energy between adjacent
Landau levels,
to be the difference in energy between adjacent
Landau levels,
![]() , then the area between the
semiclassical orbits of two adjacent
Landau levels
is given by
, then the area between the
semiclassical orbits of two adjacent
Landau levels
is given by
![]() the area
the area ![]() inside the
Landau level
inside the
Landau level ![]() is given by
is given by